A/B to multivariate testing: a tale of bias

Recently one of our customers presented us with a finding that our multivariate testing framework can be prone to bias under certain circumstances. I believe this type of bias is not unique to our system, but much more prevalent. In all these cases, reported model driven personalisation performance will be unreliable. In this article we’ll dive in and explore a few frequently occurring biases in model driven personalisation, and what can be done to prevent them.

Model driven personalisation

Model driven personalisation relies on modelling customer behavior and subsequently using these models to adapt customer experience to the individual. This process essentially starts, and ends with the user, creating a feedback loop.

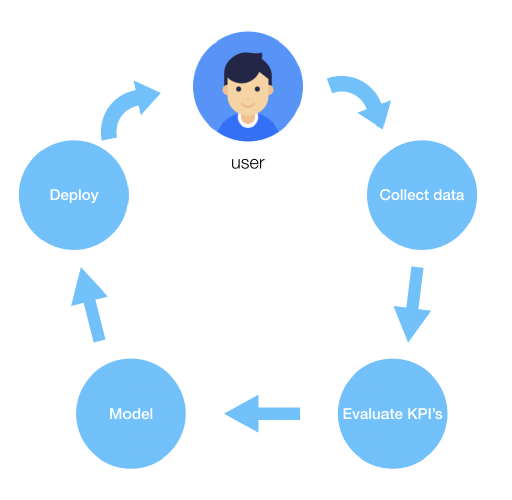
In this loop we collect user behavior, evaluate KPI’s and train models. Deploying these models to production allows our service front-end to adapt to the end user, whose response to this personalisation we collect as user behavior again, closing the loop.

At this point, we hope the personalisation has caused the user to remain on the platform longer, view more items or simply for him or her to return more often — in which case we conclude our service has improved!

The trick is to determine whether the personalised customer experience is actually responsible for any effects we observe. In the above setup, we have no way of determining whether an increase, or decrease on said KPI’s can be attributed to our efforts. Perhaps the service sees a temporary and unrelated surge in traffic, and this could very well coincide with the time we deployed our models. If this occurs, we might conclude falsely that our models are responsible for the surge — a classic example of confusing cause and correlation.

Multivariate testing

This is where multivariate testing comes in. Instead of running one variant of our service, we run multiple variants of our service simultaneously. Users that consume our service are assigned one of the variants randomly. By evaluating the same KPI’s for each variant independently at the end of the experiment we assign a ‘winning’ variant. Typically one or more of these variants will be ‘control’ groups, used as a baseline to validate any model uplifts against — precisely to rule out the correlation/cause problem described earlier.

Setting up an experiment with personalised news article recommendations, we typically assume two variants — commonly referred to as A/B testing:

• Null: No recommendations.
• Model: The scored and sorted output of a collaborate filter model.

By setting up an experiment using this approach, we are able to filter out unrelated surges or drops in traffic — ensuring we attribute any effects in user behavior to our efforts justifiably.

Bias here, bias there

However, we are still left with a problem: showing recommended articles may (and often does!) carry a placebo effect. The user group presented with recommended articles may react positively to the suggestion that the service ‘knows’ who they are. Our test at this point only verifiably shows that our users are likely to react positively to a personalised approach — we haven’t actually verified that our recommendations are any good!

To show that our recommendations are responsible for any positive uplift in KPI’s, we need to add an additional variant: the randomized control. In the case of recommendations this means that articles are assigned random scores, ordered and returned to the user. The users that are a part of this group incur the same placebo effect as the users assigned to the Model group — any difference in behavior between these two groups should now justifiably indicate true model performance. We’re now able to tell that personalised recommendations positively impact our audience, and we have also confirmed that our model actually works™!

But wait, there’s more

There is one last source of bias lurking in the details, and it depends heavily on our choice of model. In the case of a collaborative filter, where we depend on a minimum amount of behavior for each user, it is entirely possible that the model yields no recommendations for a (potentially very large) portion of our userbase. For these users we can’t show any recommendations, éven if they happen to be assigned to the Model variant.

Unfortunately then, the users that our Model variant does yield recommendations for, tend to be users that use our service regularly already. No wonder we are measuring an uplift on KPI’s for this very specific subset of our users.

The problem here is that we have no way of determining how that same subset of users behaves in the Random and Null control groups. If we were able to restore that ability, we’d be ok.

The solution then, is remarkably simple: the behavior of both Random and Null control can be adjusted to take this bias into account. For both control variants we add a boolean flag, which identifies whether the call would have yielded results if it were assigned to the Model variant. Post-hoc analysis can now effectively compare behavior of the same very specific subset of our users, across all three variants!

Tl;dr

Conventional A/B testing for model driven personalisation is fundamentally broken. At least 3 variants are needed to accurately address the placebo effect ánd the performance of your model.

Make sure that your control variants account for implicit model bias. Failure to do so will make it hard to remove model specific bias in post-hoc analysis rendering any KPI’s unreliable.